Homepage IME-USP

Imagens do projeto JOrigami recuperadas do SourceForge.

Paulo Eduardo Azevedo Silveira

O bom algoritmo

“A good algorithm is like a sharp knife: it does what it is supposed to do with a minimum amount of applied effort. Using the wrong algorithm to solve a problem is like trying to cut a steak with a screwdriver: you may eventually get a digestible result, but you will expend considerably more effort than necessary, and the result is unlikely to be aesthetically pleasing.”

— Th. Cormen, Ch. Leiserson, R. Rivest, Introduction to Algorithms

Áreas de Interesse

• Geometria Computacional - Origami Computacional
• Inteligência Artificial
• Estrutura de Dados
• Arquitetura Java

Breve Histórico

Depois de formado em Ciência da Computação, tive meu primeiro contato profissional com Java na Commworld.de, na Alemanha. Voltando ao Brasil terminei a faculdade, período em que trabalhei com projetos java, como o Panda, e participei da maratona de programação junto com meu irmão, Guilherme Silveira, que recentemente esteve na final mundial do Japão. Trabalhei em algumas consultorias até parar na Sun Microsystems onde atuei como instrutor, enquanto iniciava meu mestrado junto com o professor Coelho. Nesse meio tempo ajudei a fundar o Grupo de Usuários Java, o maior fórum de Java em língua portuguesa. Atualmente atuo na Caelum, uma empresa focada em computação, consultoria e treinamento.

Cursos de verão da USP

Desde 2004 ajudo e ministro alguns dos cursos de verão da USP, no que se refere as disciplinas que envolvem Java. Em 2005 criamos o novo curso de Algoritmos em Java e finalmente teremos um material para ele.

Atualmente são diversos os instrutores dos cursos, a maioria deles envolvidos na Caelum e na USP. Você pode fazer download do material usado como referência:

• Java básico: caelum-java-objetos-fj11.pdf
• Java distribuído/web: caelum-java-web-fj21.pdf
• Algoritmos e Estrutura de Dados: estava previsto

Matemática e Algoritmos sobre as Dobras

Foi o tema do meu mestrado que defendi no início de 2007, orientado pelo professor doutor José Coelho de Pina.

Origami computacional é um ramo recente da ciência da computação que estuda algoritmos eficientes para problemas envolvendo dobras. Esse ramo, essencialmente, nasceu há quase 15 anos com o trabalho de Robert J. Lang em que métodos computacionais são empregados no auxílio do projeto de modelos de origami. Desde o trabalho de Lang, origami computacional tem crescido muito, devido ao esforço de vários pesquisadores.

A dissertação trata de alguns aspectos matemáticos e algorítmicos de problemas envolvendo dobras. A relação entre as construções geométricas clássicas com régua e compasso e a geometria das construções com dobras é apresentada, a complexidade computacional de alguns problemas relacionados é considerada e uma solução do problema de dobrar e cortar é descrita.

JOrigami: o problema de dobrar e cortar

Juntamente com Rafael Cosentino, Deise Aoki e o professor Coelho, fizemos uma implementação do problema de dobrar e cortar, o JOrigami.

Esse problema pode ser citado da seguinte maneira: dado um polígono como entrada, podemos dobrar o papel de tal maneira que com apenas um corte reto teremos o nosso polígono como resultado ao abrir o papel? O incrível é que isso é sempre possível, e o algoritmo gera as dobras para tal feito. David Eppstein, um dos autores do artigo em que baseamos nossa solução, blogou sobre nós. Marshal Bern, Barry Hayes e Joseph O’Rourke também nos ajudaram e trocamos emails.

O grande peixe: passo a passo

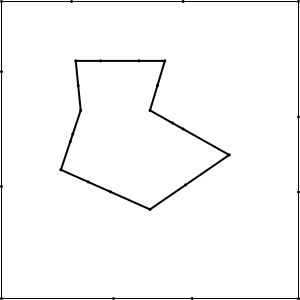
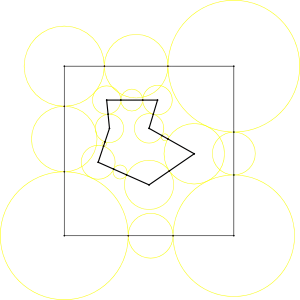
Polígono, posicionamento inicial dos discos (automático, pode ser feito manualmente), cobertura completa das arestas.

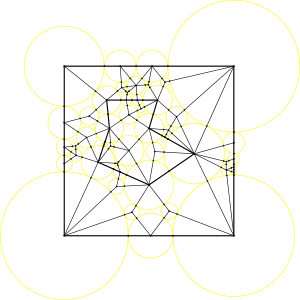
Cobertura fixa das arestas e faces divididas, particionamento em quadriláteros e triângulos, a árvore.

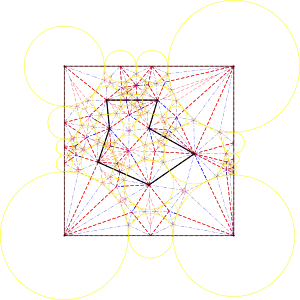
Crease pattern, crease pattern com mountain-valley assignment, crease pattern e discos.

Uma estrela (não centralizada)

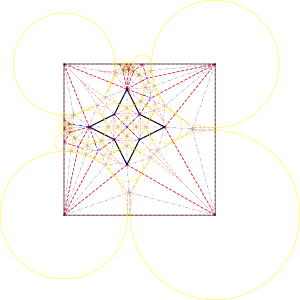
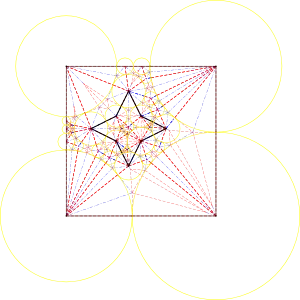
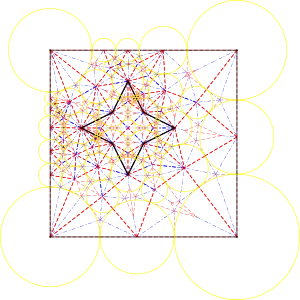
Manual initial packing, Biggest Neighbor, 474 dobras. Min distance, Median disk, 564 dobras. Sem otimização inicial, biggest neighbor, 1184 dobras.

O tamanho do papel pode fazer uma grande diferença, mas as moléculas que não tocam o polígono não precisam ser dobradas.

Outras imagens

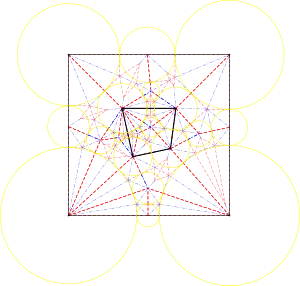
Artigos de referência

• On the Mathematics of Flat Origami, Thomas Hull
• When Can you fold a Map?, Erik Demaine et al.
• Complexity of flat Origamis, Marshal Bern e Barry Hayes
• A computational algorithm for Origami Design, Robert J. Lang
• A Disk-Packing Algorithm for an Origami Magic Trick, Erik Demaine, Marshal Bern, Barry Hayes e David Eppstein

Também há o livro Geometric Folding Algorithms: Linkages, Origami, and Polyhedra, escrito por Demaine e O’Rourke. Um capítulo inteiro é dedicado ao problema de dobrar e cortar.

Colegas

• Renato Lucindo
• Ricardo Hermann (de onde copiei o layout!)
• Rafael Cosentino
• André Andrade
• Domingos Soares Neto
• Marcel Kenji
• Carlos Cardonha
• Wanderley Guimarães

Contato

peas arroba ime usp br